Тело массой m = 560 г двигалось по гладкой поверхности со скоростью
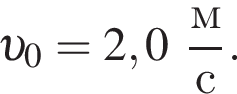 В момент времени t0 = 0 с на тело в направлении его движения начинает действовать сила
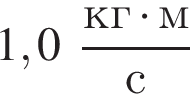
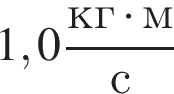
В момент времени t0 = 0 с на тело в направлении его движения начинает действовать сила ![]() модуль которой линейно зависит от времени (см. рис.). Скорость тела достигнет значения
модуль которой линейно зависит от времени (см. рис.). Скорость тела достигнет значения 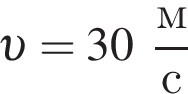 в момент времени t, равный ... с.
в момент времени t, равный ... с.
Два тела массами m1 = m и m2 = 2m двигались во взаимно перпендикулярных направлениях со скоростями, модули которых соответственно равны 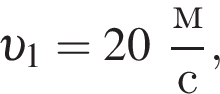
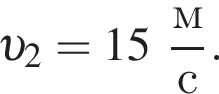 Если после соударения тела начали двигаться как единое целое, то модуль их скорости υ после соударения равен ...
Если после соударения тела начали двигаться как единое целое, то модуль их скорости υ после соударения равен ... ![]()
Два тела массами m1 = m и m2 = 2m двигались во взаимно перпендикулярных направлениях со скоростями, модули которых соответственно равны 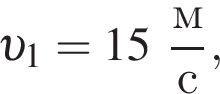
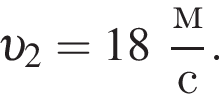 Если после соударения тела начали двигаться как единое целое, то модуль их скорости υ после соударения равен ...
Если после соударения тела начали двигаться как единое целое, то модуль их скорости υ после соударения равен ... ![]()
Два тела массами m1 = 2,00 кг и m2 = 1,50 кг, модули скоростей которых одинаковые (υ1 = υ2), движутся по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой υ = 10 м/c, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Шайба массой  подлетела к вертикальному борту хоккейной коробки и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним:
подлетела к вертикальному борту хоккейной коробки и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним:  Если модуль изменения импульса шайбы
Если модуль изменения импульса шайбы 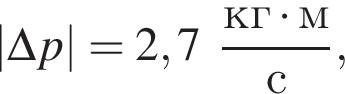 то модуль скорости шайбы υ2 непосредственно после ее удара о борт равен:
то модуль скорости шайбы υ2 непосредственно после ее удара о борт равен:
На гладкой горизонтальной поверхности лежит брусок массой 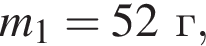 прикрепленный к стене невесомой пружиной жесткостью
прикрепленный к стене невесомой пружиной жесткостью 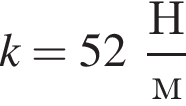 (см.рис.). Пластилиновый шарик массой
(см.рис.). Пластилиновый шарик массой  летящий горизонтально вдоль оси пружины со скоростью, модуль которой
летящий горизонтально вдоль оси пружины со скоростью, модуль которой 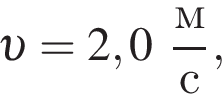 попадает в брусок и прилипает к нему. Максимальное сжатие пружины
попадает в брусок и прилипает к нему. Максимальное сжатие пружины ![]() равно ... мм.
равно ... мм.
К вертикальному борту хоккейной коробки подлетела шайба со скоростью, модуль которой 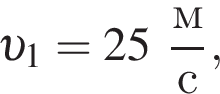 и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним: υ2=υ1. Если модуль изменения импульса шайбы при ударе о борт
и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним: υ2=υ1. Если модуль изменения импульса шайбы при ударе о борт 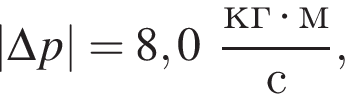 то масса m шайбы равна:
то масса m шайбы равна:
На гладкой горизонтальной поверхности лежит брусок массой m1 = 60 г, прикрепленный к стене невесомой пружиной жесткостью 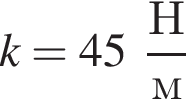 (см.рис.). Пластилиновый шарик массой m2 = 60 г, летящий горизонтально вдоль оси пружины, попадает в брусок и прилипает к нему. Если максимальное сжатие пружины
(см.рис.). Пластилиновый шарик массой m2 = 60 г, летящий горизонтально вдоль оси пружины, попадает в брусок и прилипает к нему. Если максимальное сжатие пружины  то модуль начальной скорости υ шарика непосредственно перед попаданием в брусок равен ...
то модуль начальной скорости υ шарика непосредственно перед попаданием в брусок равен ... ![]()
Металлический шарик падает вертикально вниз на горизонтальную поверхность стальной плиты со скоростью, модуль которой 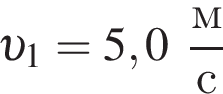 и отскакивает от нее вертикально вверх с такой же по модулю скоростью:
и отскакивает от нее вертикально вверх с такой же по модулю скоростью:  Если масса шарика
Если масса шарика 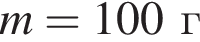 то модуль изменения импульса
то модуль изменения импульса ![]() шарика при ударе о плиту равен:
шарика при ударе о плиту равен:
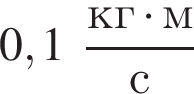
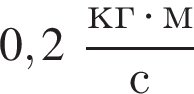
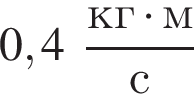

На гладкой горизонтальной поверхности лежит брусок массой m1, прикрепленный к стене невесомой пружиной жесткостью 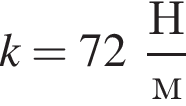 (см.рис.). Пластилиновый шарик массой
(см.рис.). Пластилиновый шарик массой  летящий горизонтально вдоль оси пружины со скоростью, модуль которой
летящий горизонтально вдоль оси пружины со скоростью, модуль которой 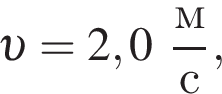 попадает в брусок и прилипает к нему. Если максимальное сжатие пружины
попадает в брусок и прилипает к нему. Если максимальное сжатие пружины  то масса m1 бруска равна ... г.
то масса m1 бруска равна ... г.
Шайба массой  подлетела к вертикальному борту хоккейной коробки и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним:
подлетела к вертикальному борту хоккейной коробки и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним:  Если модуль изменения импульса шайбы
Если модуль изменения импульса шайбы 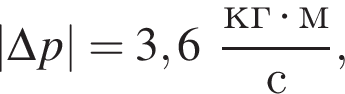 то модуль скорости шайбы υ2 непосредственно после ее удара о борт равен:
то модуль скорости шайбы υ2 непосредственно после ее удара о борт равен:
На гладкой горизонтальной поверхности лежит брусок массой  прикрепленный к стене невесомой пружиной жесткостью
прикрепленный к стене невесомой пружиной жесткостью 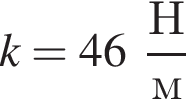 (см.рис.). Пластилиновый шарик массой
(см.рис.). Пластилиновый шарик массой  летящий горизонтально вдоль оси пружины со скоростью, модуль которой
летящий горизонтально вдоль оси пружины со скоростью, модуль которой 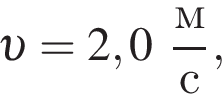 попадает в брусок и прилипает к нему. Максимальное сжатие пружины
попадает в брусок и прилипает к нему. Максимальное сжатие пружины ![]() равно ... мм.
равно ... мм.
Металлический шарик массой 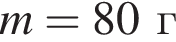 падает вертикально вниз на горизонтальную поверхность стальной плиты и отскакивает от нее вертикально вверх с такой же по модулю скоростью:
падает вертикально вниз на горизонтальную поверхность стальной плиты и отскакивает от нее вертикально вверх с такой же по модулю скоростью:  Если непосредственно перед падением на плиту модуль его скорости
Если непосредственно перед падением на плиту модуль его скорости 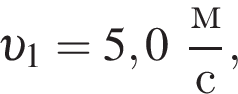 то модуль изменения импульса
то модуль изменения импульса ![]() шарика при ударе о плиту равен:
шарика при ударе о плиту равен:
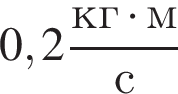
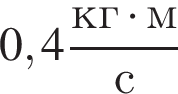
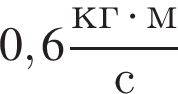
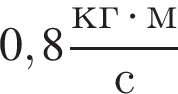
На гладкой горизонтальной поверхности лежит брусок массой  прикрепленный к стене невесомой пружиной жесткостью
прикрепленный к стене невесомой пружиной жесткостью 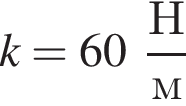 (см.рис.). Пластилиновый шарик массой
(см.рис.). Пластилиновый шарик массой  летящий горизонтально вдоль оси пружины со скоростью, модуль которой
летящий горизонтально вдоль оси пружины со скоростью, модуль которой 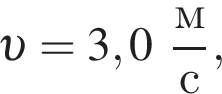 попадает в брусок и прилипает к нему. Максимальное сжатие пружины
попадает в брусок и прилипает к нему. Максимальное сжатие пружины ![]() равно ... мм.
равно ... мм.
Два тела массами m1 = 4,00 кг и m2 = 3,00 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 10,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Два тела массами m1 = 6,00 кг и m2 = 8,00 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 10,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Два тела массами m1 = 6,00 кг и m2 = 8,00 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 5,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Пять вагонов, сцепленных друг с другом и движущихся со скоростью, модуль которой 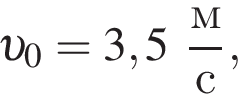 столкнулись с двумя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
столкнулись с двумя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
Два тела массами m1 = 4,00 кг и m2 = 3,00 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 15,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Два тела массами m1 = 2,00 кг и m2 = 1,50 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 5,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Четыре вагона, сцепленные друг с другом и движущиеся со скоростью, модуль которой 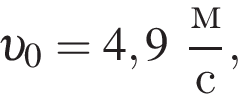 столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
Два вагона, сцепленные друг с другом и движущиеся со скоростью, модуль которой 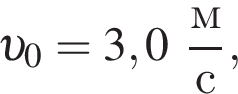 столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
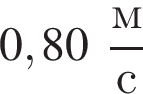
Четыре вагона, сцепленные друг с другом и движущиеся со скоростью, модуль которой 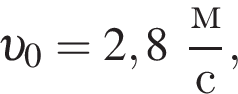 столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости υ будет равен:
Три вагона, сцепленные друг с другом и движущиеся со скоростью, модуль которой 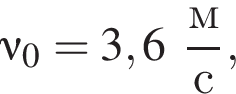 столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости
столкнулись с тремя неподвижными вагонами. Если массы всех вагонов одинаковы, то после срабатывания автосцепки модуль их скорости ![]() будет равен:
будет равен:
В брусок, лежавший на гладкой горизонтальной поверхности и прикрепленный к вертикальному упору легкой пружиной жесткости k = 1,2 кН/м, попадает и застревает в нем пуля массы m2 = 0,01 кг, летевшая со скоростью, модуль которой υ = 56 м/с, направленной вдоль оси пружины (см. рис.). Если максимальное значение силы, которой пружина действует на упор в процессе возникших колебаний, Fmax = 13,7 Н, то масса m1 бруска равна ... кг. Ответ округлите до целого.
В брусок массы m1 = 2,0 кг, лежавший на гладкой горизонтальной поверхности и прикрепленный к вертикальному упору легкой пружиной жесткости k = 1,6 кН/м, попадает и застревает в нем пуля массы m2 = 10 г, летевшая со скоростью, модуль которой υ = 60 м/с, направленной вдоль оси пружины (см. рис.). Максимальное значение модуля абсолютного удлинения Δlmax пружины равно ... мм.
В брусок массы m1 = 2,0 кг, лежавший на гладкой горизонтальной поверхности и прикрепленный к вертикальному упору легкой пружиной, попадает и застревает в нем пуля массы m2 = 0,01 кг, летевшая со скоростью, модуль которой υ = 60 м/с, направленной вдоль оси пружины (см. рис.). Если максимальное значение силы, которой пружина действует на упор в процессе возникших колебаний, Fmax = 15,5 Н, то жесткость k пружины равна ... кН/м. Ответ округлите до целого.
Находящийся на шкафу кот массой m1 = 3,0 кг запрыгивает на светильник, расположенный на расстоянии L = 100 см от шкафа (см. рис.). Начальная скорость кота направлена горизонтально. Светильник массой m2 = 2,0 кг подвешен на невесомом нерастяжимом шнуре на расстоянии H1=140 см от потолка. Расстояние от потолка до шкафа H2 = 95 см. Если пренебречь размерами кота и светильника, то максимальное отклонение светильника с котом от положения равновесия в горизонтальном направлении будет равно ... см.
Примечание. Колебания светильника с котом нельзя считать гармоническими.
Находящийся на шкафу кот массой m1 = 2,0 кг запрыгивает на светильник, расположенный на расстоянии L = 120 см от шкафа (см. рис.). Начальная скорость кота направлена горизонтально. Светильник массой m2 = 4,0 кг подвешен на невесомом нерастяжимом шнуре на расстоянии H1=120 см от потолка. Расстояние от потолка до шкафа H2 = 80 см. Если пренебречь размерами кота и светильника, то максимальное отклонение светильника с котом от положения равновесия в горизонтальном направлении будет равно ... см.
Примечание. Колебания светильника с котом нельзя считать гармоническими.
Два тела массами m1 и m2 = 3m1 двигались по гладкой горизонтальной м плоскости со скоростями, модули которых 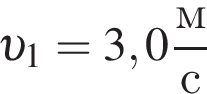 и
и 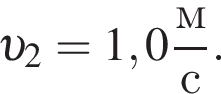 Если после столкновения тела продолжили движение как единое целое, то модуль максимально возможной скорости υ тел непосредственно после столкновения равен:
Если после столкновения тела продолжили движение как единое целое, то модуль максимально возможной скорости υ тел непосредственно после столкновения равен:
В начальный момент времени импульс частицы был равен ![]() Через некоторое время импульс частицы стал равен
Через некоторое время импульс частицы стал равен ![]() (см. рис.). Изменение импульса частицы
(см. рис.). Изменение импульса частицы ![]() —
—
В начальный момент времени импульс частицы был равен ![]() Через некоторое время импульс частицы стал равен
Через некоторое время импульс частицы стал равен ![]() (см. рис.). Изменение импульса частицы
(см. рис.). Изменение импульса частицы ![]() —
—

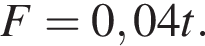 Изменение импульса тела равно площади фигуры под графиком
Изменение импульса тела равно площади фигуры под графиком 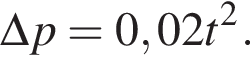 Поскольку
Поскольку 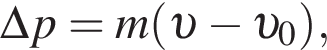 то момент времени равен
то момент времени равен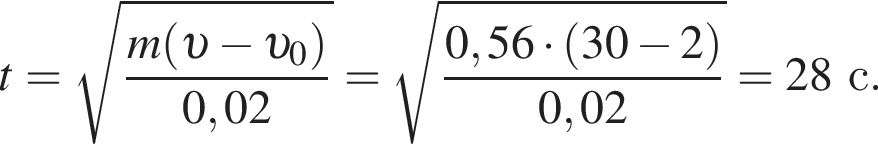
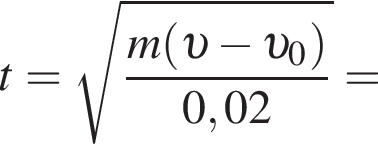
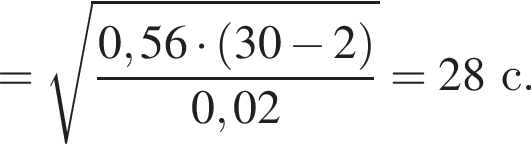
 Учитывая, что скорости тел до взаимодействия были перпендикулярны, получаем:
Учитывая, что скорости тел до взаимодействия были перпендикулярны, получаем: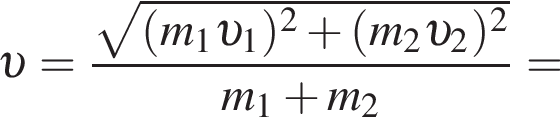
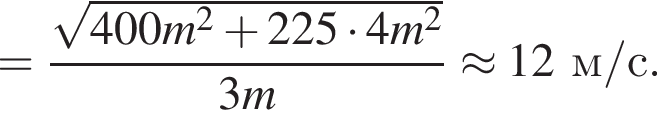
 Учитывая, что скорости тел до взаимодействия были перпендикулярны, получаем:
Учитывая, что скорости тел до взаимодействия были перпендикулярны, получаем: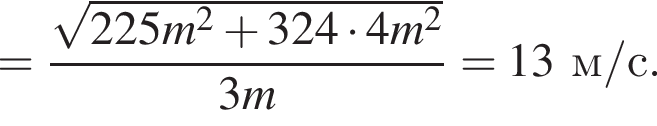
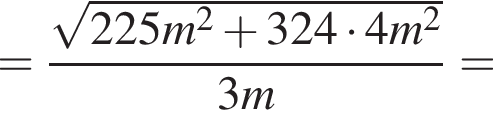
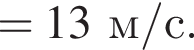
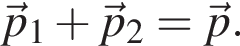 Поскольку до столкновения тела движутся во взаимно перпендикулярных направлениях по теореме Пифагора получаем
Поскольку до столкновения тела движутся во взаимно перпендикулярных направлениях по теореме Пифагора получаем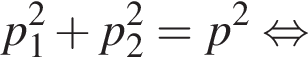
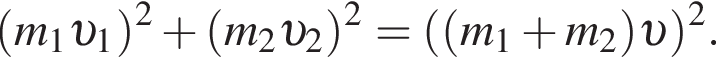
 :
: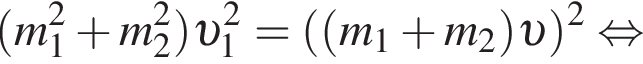
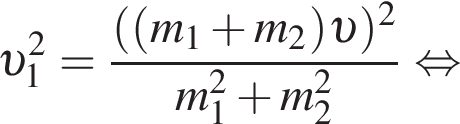
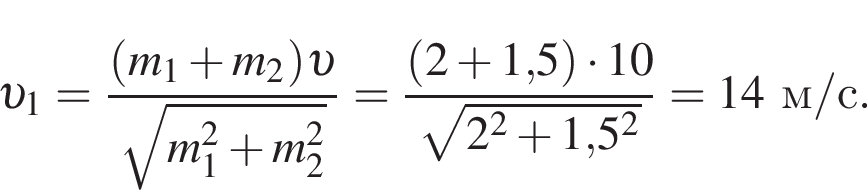
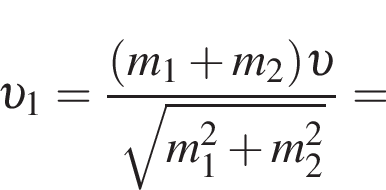
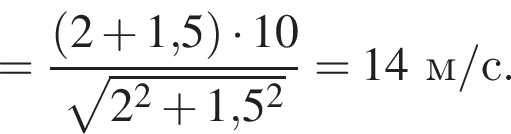
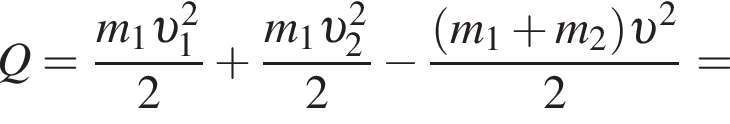
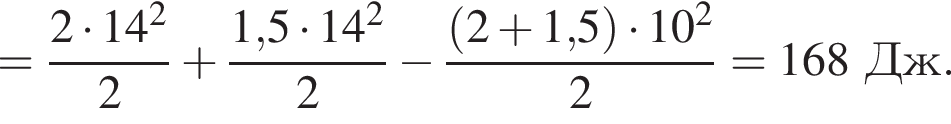
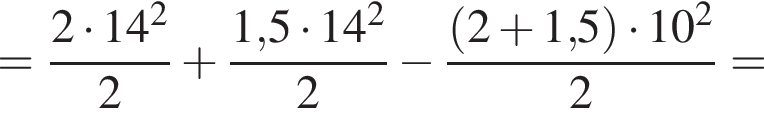
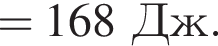
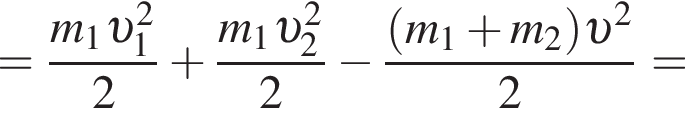
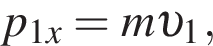
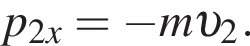
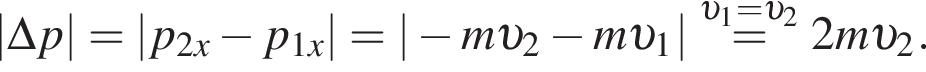
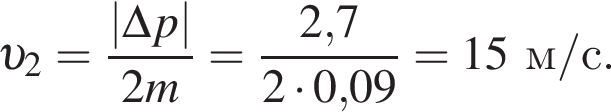
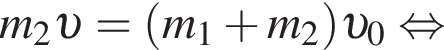
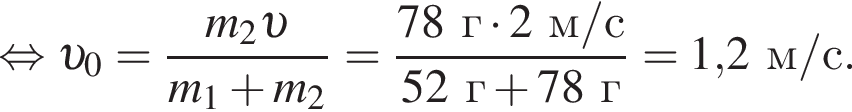
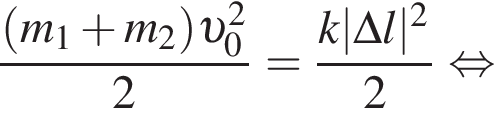
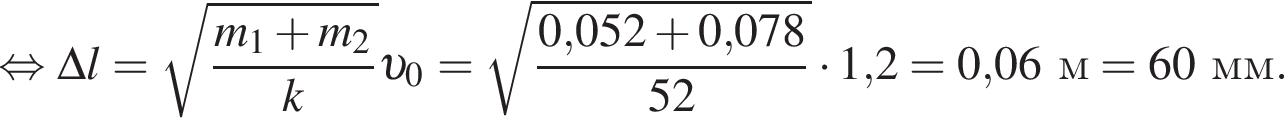
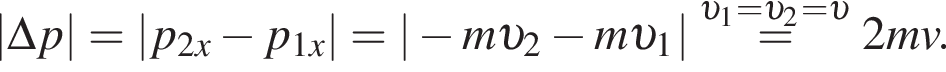
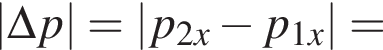
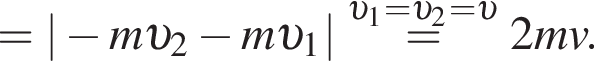
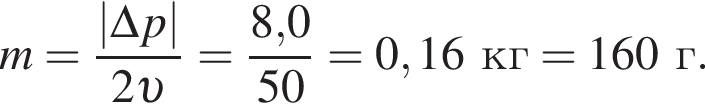
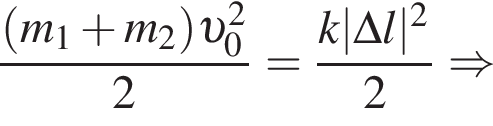
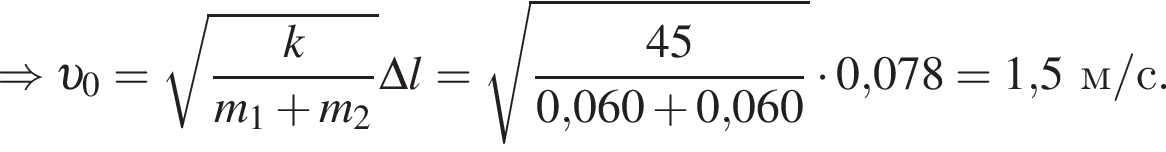
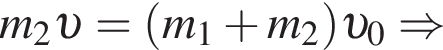
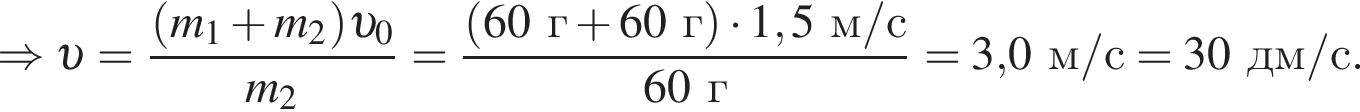
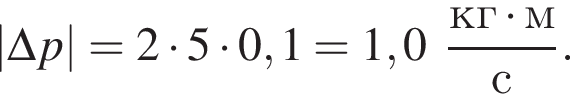
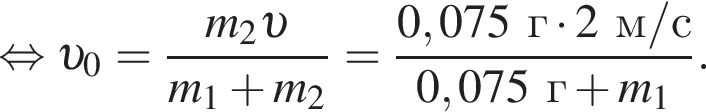
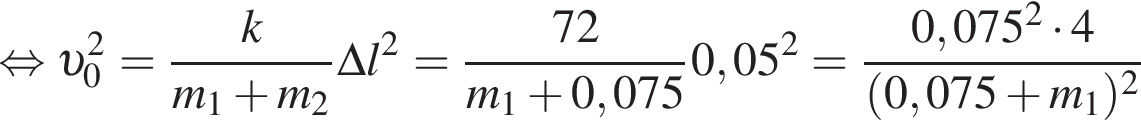
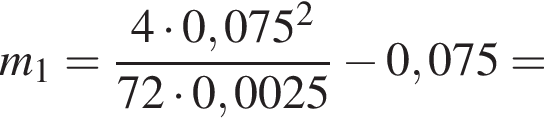



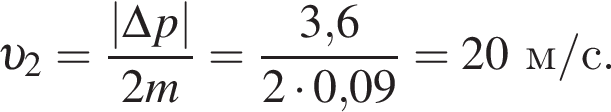
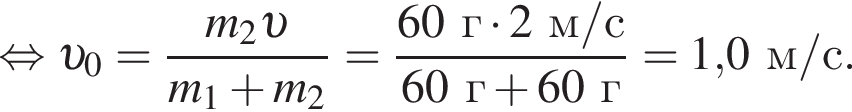
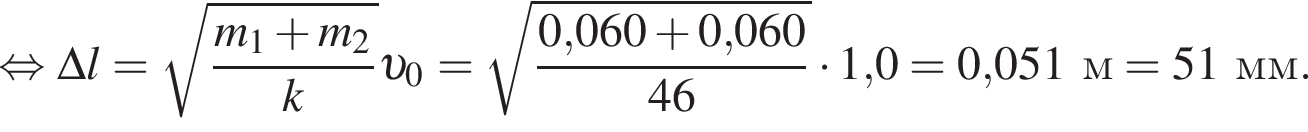
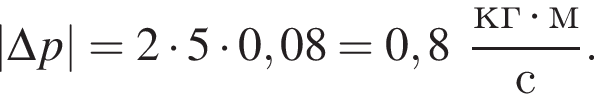
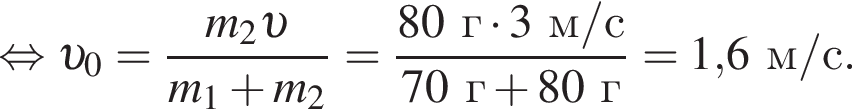
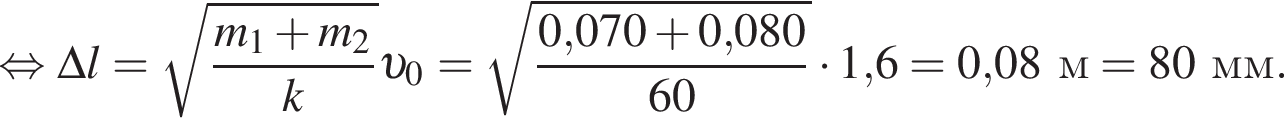
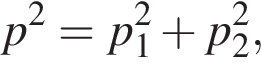
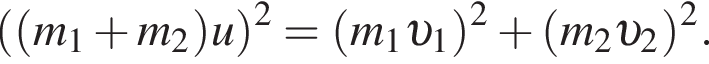
 получаем:
получаем: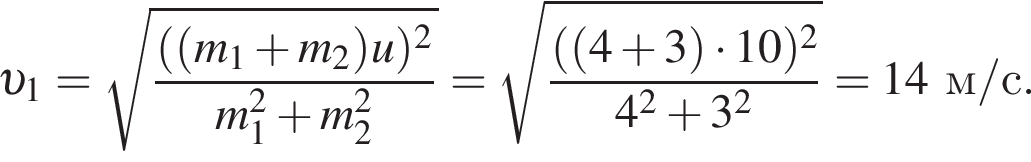
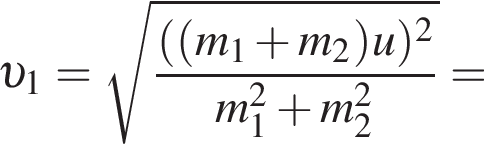
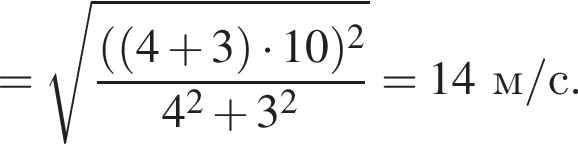
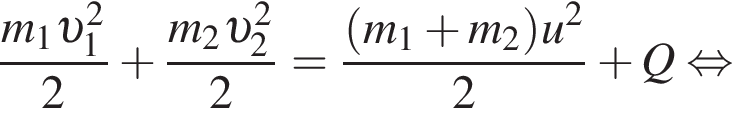

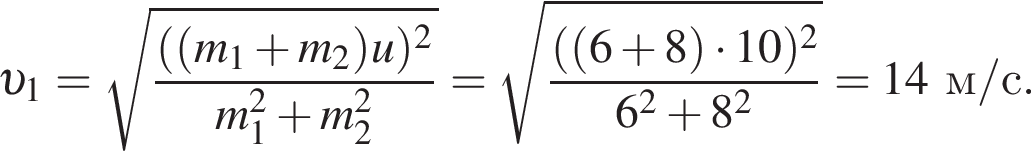
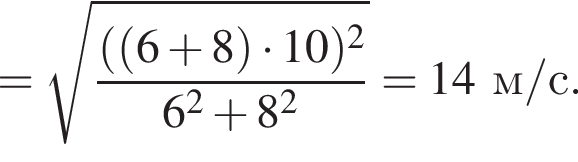
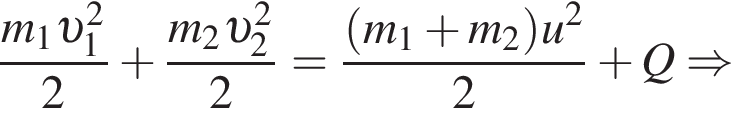
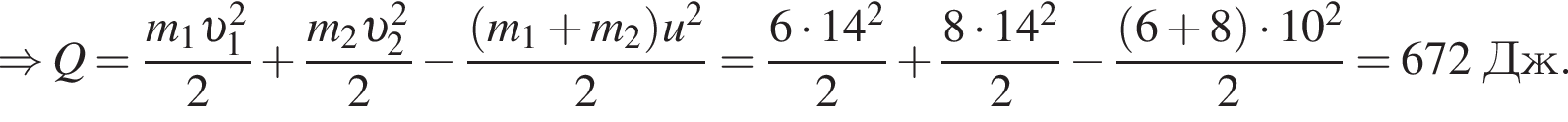
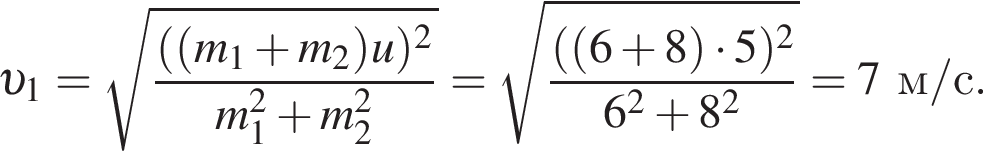
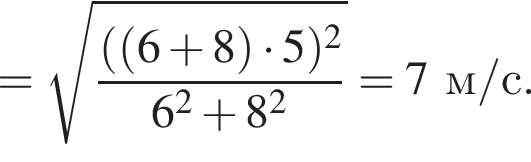
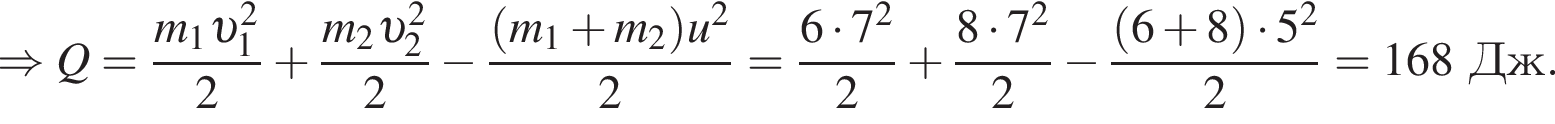
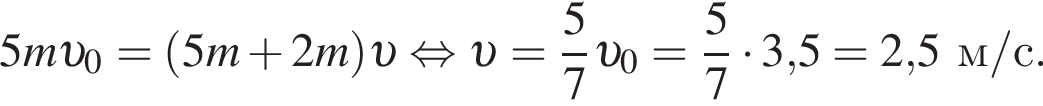
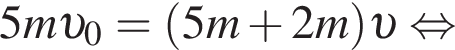
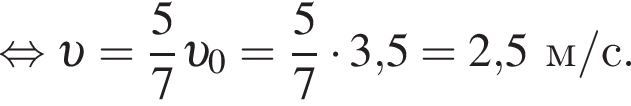
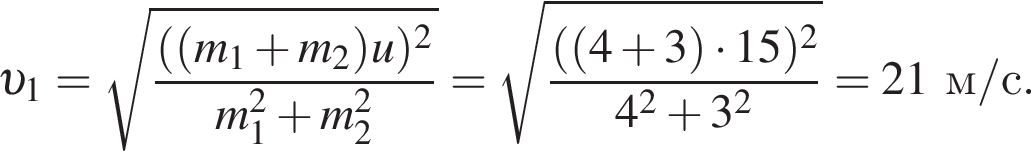
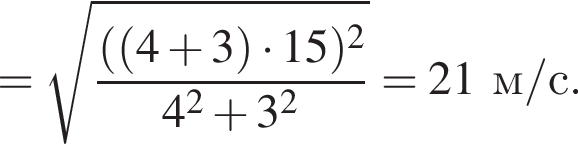
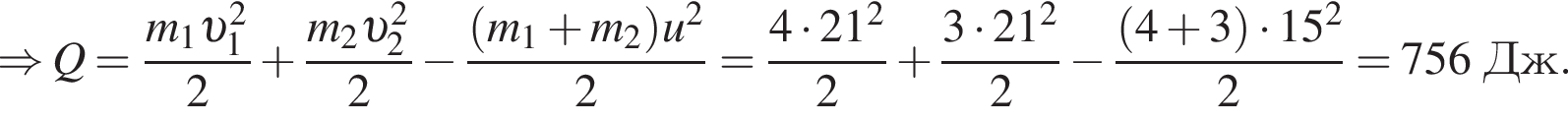
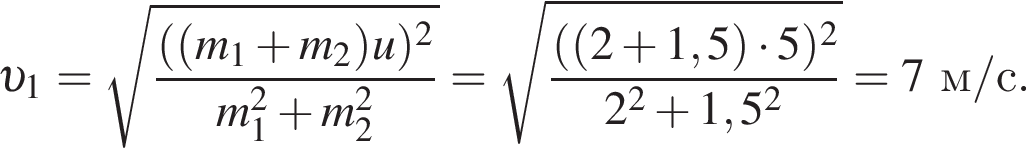
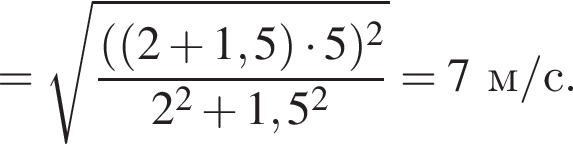
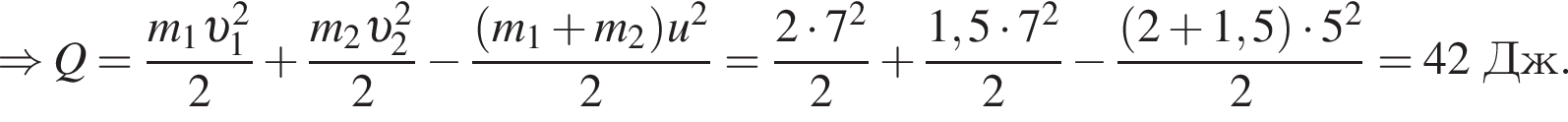
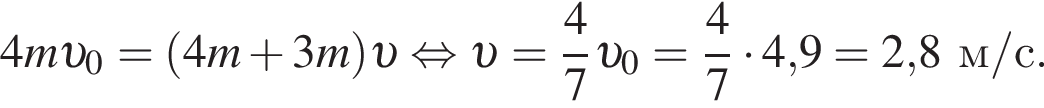
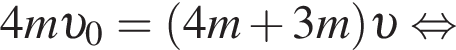
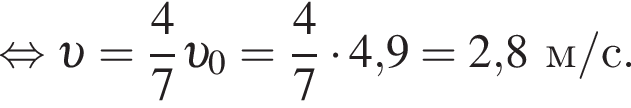
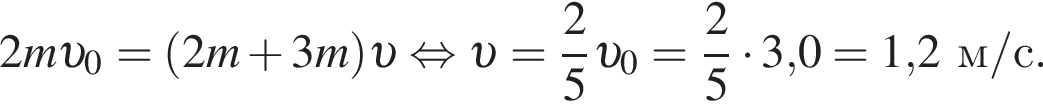
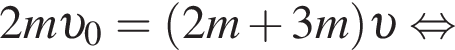
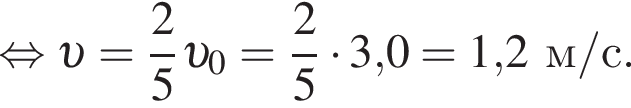
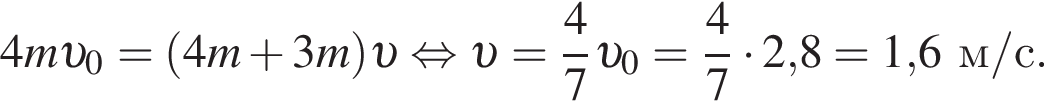
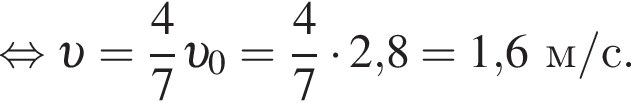
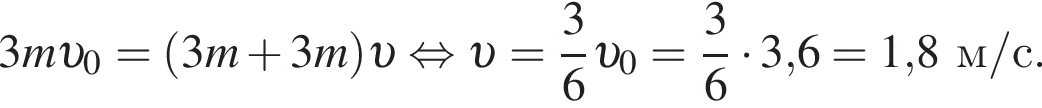
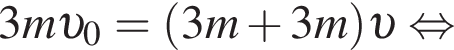
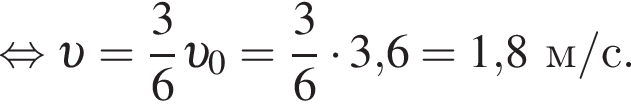
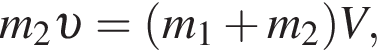
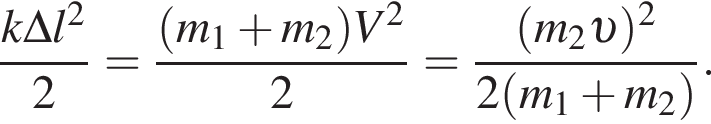
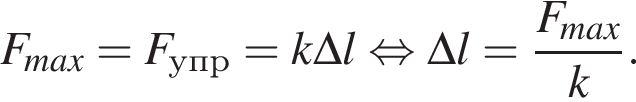
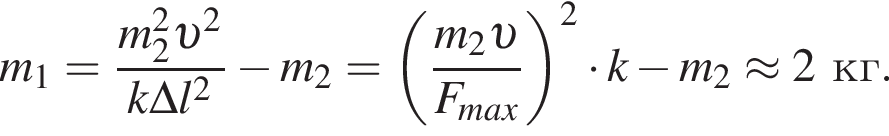
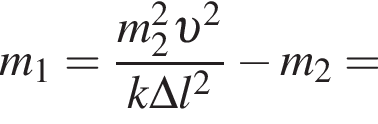
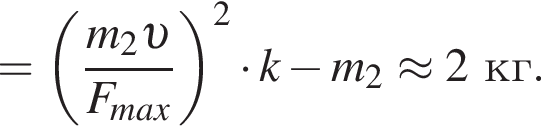
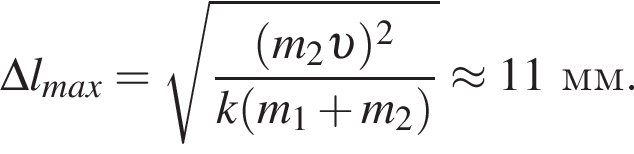
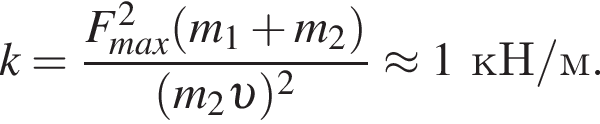
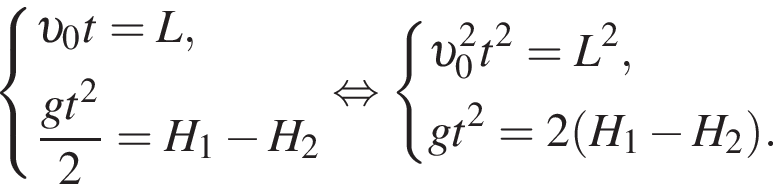
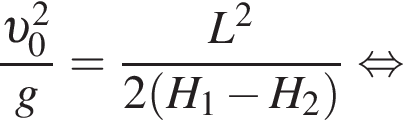
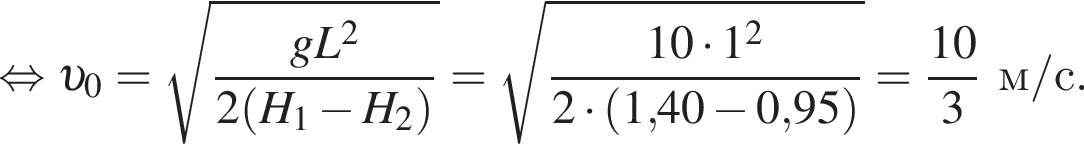
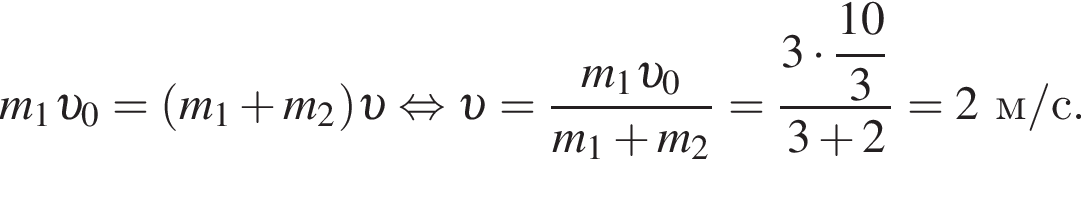
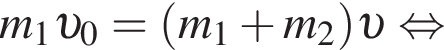
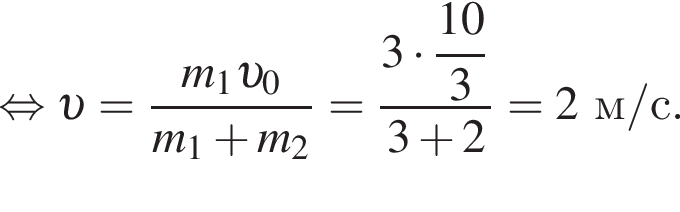
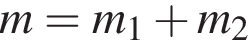 ):
):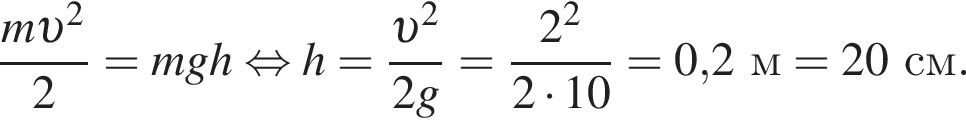
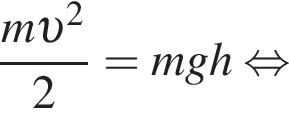
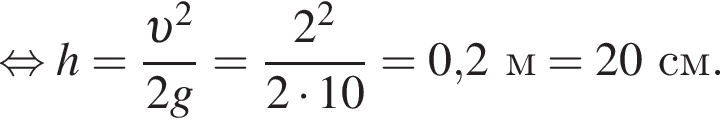
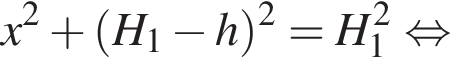
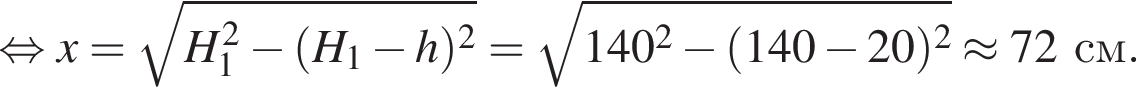
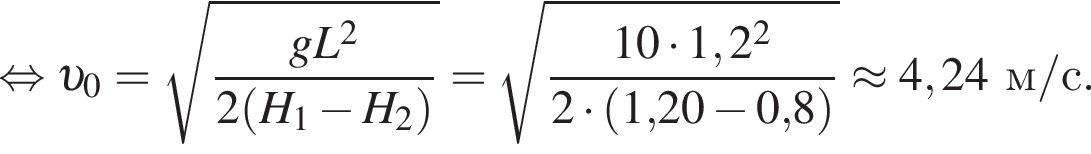
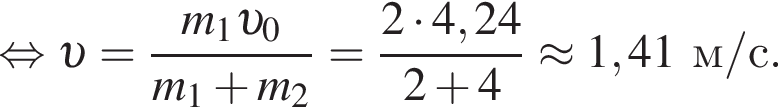
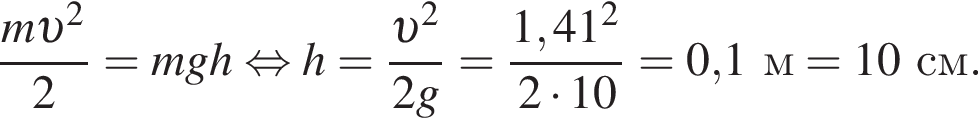
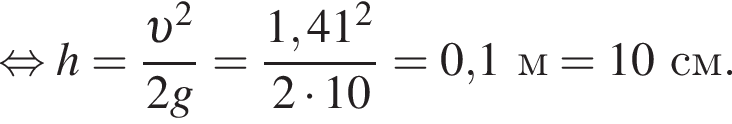
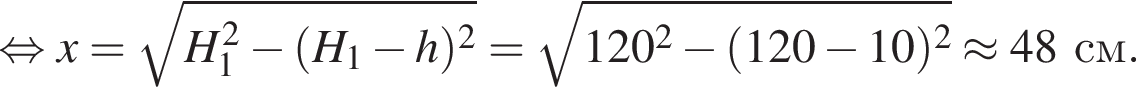
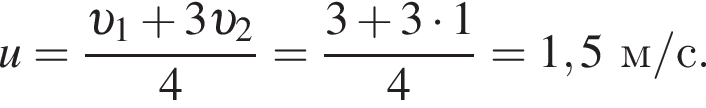
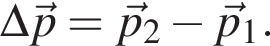 По правилу сложения векторов он направлен в сторону, противоположную векторам и по модулю равен разности модулей векторов.
По правилу сложения векторов он направлен в сторону, противоположную векторам и по модулю равен разности модулей векторов.